Influence of Particle Size and True Density of Hollow Glass Microspheres on the Compression Strength

This application note explores the correlation between particle size, true density, and compressive strength of hollow glass microspheres (HGMs). Utilizing Bettersizer 2600 laser diffraction particle size analyzer and BetterPyc 380 gas pycnometer, it confirms that particle size and true density affect the compressive strength. The insights provided by Bettersize contribute significantly to the field of HGMs material engineering.

 

Product	Bettersizer 2600, BetterPyc 380
Industry	Ceramics
Sample	Hollow glass microsphere
Measurement Type	Particle size, Particle Distribution, True Density
Measurement Technology	Laser Diffraction, Gas Displacement Method

 

Jump to a section: 

• Introduction
• Measurement Method
• Result
• Conclusion
• Reference

 

---

Introduction 

Hollow Glass Microspheres (HGMs) are inorganic nonmetallic spherical materials manufactured through specified processes, typically with diameters ranging from 10 to 250 µm and wall thicknesses of 1 to 2 µm as shown in Figure 1. These microspheres are renowned for their exceptional properties, such as abrasion resistance, corrosion resistance, radiation shielding, low water absorption, and chemical stability. They can be widely utilized as composite material fillers in construction, rubber, coatings, marine, aerospace, and other fields. The compressive strength of HGMs is a crucial physical parameter directly influencingtheir applicability and the quality of end products in various fields. 

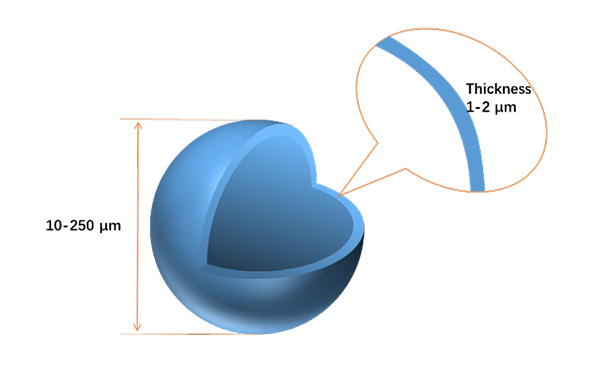
Figure 1. HGM structure

 

According to the theoretical fracture strength formula for an individual hollow glass microsphere [1,2]:

 

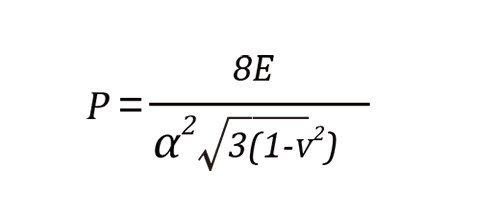
P is the compressive strength 

α is the shape factor (the ratio of diameter D to wall thickness t)

E is the theoretical Young's modulus for the HGM 

ν is the Poisson's ratio of the wall materials

 

The compressive strength of HGMs is related to diameter D and wall thickness t, as these factors collectively influence the shape factor. Since HGMs powder consists of numerous particles of different sizes, the comprehensive effect of particle size and distribution needs to be considered. Directly measuring the wall thickness of HGMs is a time consuming task, but evaluating its thickness through true density measurement will be more feasible. Accurate measurement and analysis of both particle size distribution and true density of HGMs powders help in better understanding their performance in different applications, optimizing filling quantity and methods, and further enhancing the performance and stability of composite materials.

 

Measurement Method 

This study employed the Bettersizer 2600 laser diffraction particle size analyzer and BetterPyc 380 gas pycnometer to investigate the particle size distribution and true density of four sets of identical formulations of HGMs. The test results were analyzed to explore the relationship among compressive strength, particle size distribution and true density.

The Bettersizer 2600, based on Mie theory (compliant with ISO 13320), quickly acquires particle size and distribution information by measuring the diffraction angle and intensity of particles against the laser as shown in Figure 2. It offers rapid testing speeds, with data results available in just 1 minute. With wet method, the refraction index of the HGMs and solvent media (distilled water) was 1.46 and 1.33, respectively.

 

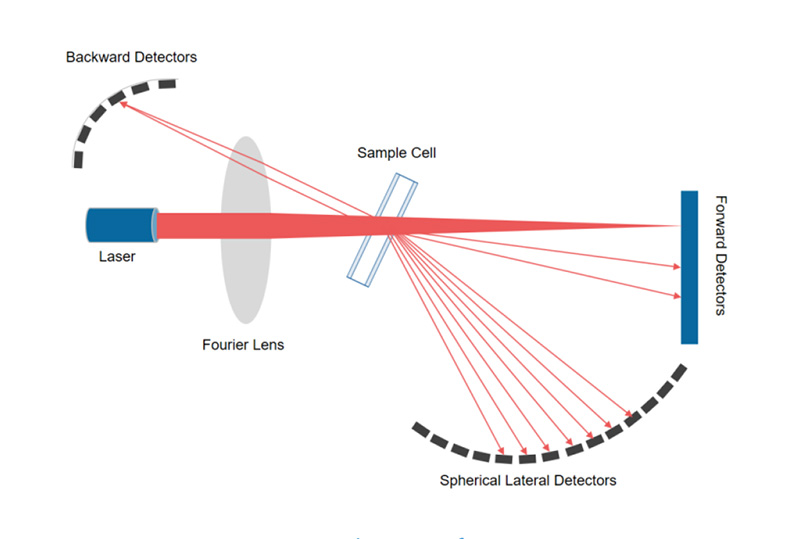
Figure 2. System diagram of Bettersizer 2600

 

The BetterPyc 380 gas pycnometer is based on the ideal gas state equation and utilizes the gas displacement method (compliant with ISO 12154:2014) with temperature control system. It allows for the measurement of the HGMs’ volume and subsequently its true density. Helium is employed as the analytical gas in this study, with measurements conducted at pressures of 19.5 psig and a controlled equilibrium rate of 0.005 psig/min at a temperature of 20. The instrument offers fast testing speeds and is operates non-destructively, rendering it an efficient and reliable method for density testing.

 

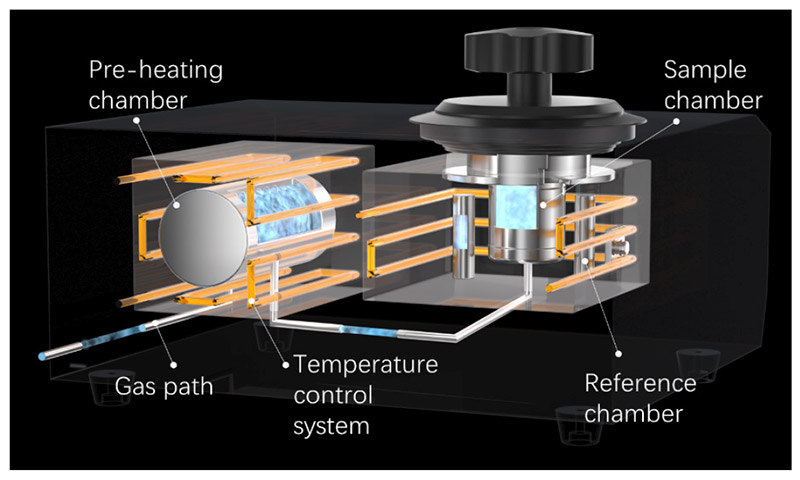
Figure 3. System diagram of BetterPyc 380

 

Result 

Table 1 presents the typical particle size and true density data of four sample groups. It is observed that samples HGM-1 and HGM-2 have similar particle sizes and distributions, with true densities of 0.6033 g/cm3 and 0.3842 g/cm3 respectively. Their compressive strengths are 83 MPa and 38 MPa respectively. According to the theoretical fracture strength formula, when the diameter remains constant, a higher true density indicates a thicker wall thickness, resulting in a smaller shape factor and subsequently increasing compressive strength. The experimental findings align well with the theoretical expectations.

 

Sample	Particle Size Distribution (µm)			True Density  (g/cm3 )	Compression Strength  (MPa)
	D10	D50	D90
HGM-1	16.62	40.57	79.76	0.6033	83
HGM-2	16.34	40.48	79.82	0.3842	38
HGM-3	12.09	20.43	33.12	0.5033	110
HGM-4	4.51	10.11	21.06	0.7824	207

Table 1. The particle size distribution, true density and compression strength of HGMs samples.

 

By comparing HGM-2, HGM-3 and HGM-4, as illustrated in Figure 4, it becomes apparent that as the particle size D50 decreases, both the true density (indicated by wall thickness) gradually increases, signifying a smaller shape factor. This phenomenon accounts for the increase in compressive strength. This observation underscores the importance of particle size and density in determining the mechanical properties of hollow glass microspheres.

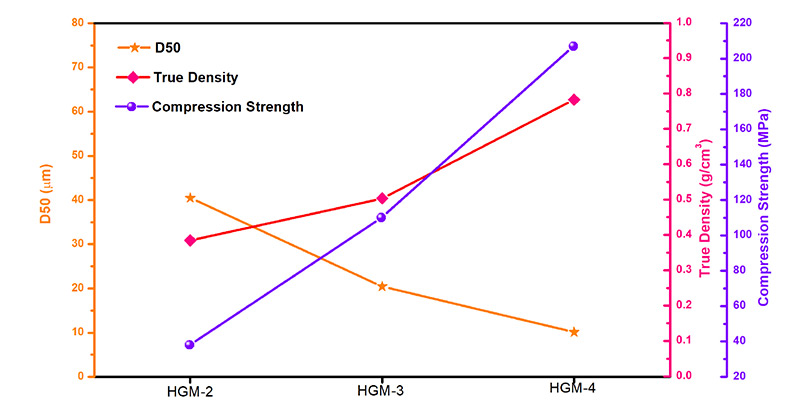
Figure 4. D50, True density and compression strength of HGM-2, HGM-3 and HGM-4

 

Conclusion 

In summary, for HGMs with the same formulation, controlling different particle size ranges through sieving allows the production of samples with varying strength characteristics. To meet specific particle size criteria, optimizing the process to enhance the true density of hollow glass microspheres is a viable approach, which can potentially enhance their compressive strength. The Bettersizer 2600 laser particle size analyzer and BetterPyc 380 gas pycnometer designed by Bettersize can provide essential references and monitor for material design and engineering applications.

 

Bettersizer 2600

BetterPyc 380

 

Reference 

[1] P.W. Bratt, J. Cunnion, B.D. Spivack, Advances in Materials Characterization 441 (1983). 
[2] S.P. Timoshenko, J.M. Gere, Theory of Elastic Stability, McGraw-Hill, New York, 1961.

 

 

About the Authors

	Perfil Liu Senior Application Engineer @ Bettersize Instruments
	Yanling Qu Application Engineer @ Bettersize Instruments