Динамическое рассеяние света

Введение

Динамическое рассеяние света (ДРС), также известное как фотонная корреляционная спектроскопия (ФКС), является широко используемым методом определения характеристик наночастиц. Анализатор размера частиц DLS обладает такими преимуществами, как точность, быстрота и хорошая повторяемость при измерении наночастиц, эмульсий или суспензий. Сайт BeNano 180 Zeta Pro анализатор наночастиц основан на динамическом рассеянии света. Он может измерять размеры наноматериалов вплоть до 0,3 нанометра, что является необходимым инструментом для измерения распределения размеров наночастиц для понимания и исследования нанопорошковых материалов.

Теоретическая основа

Что такое рассеяние света? Когда монохроматический и когерентный источник света облучает частицу, электромагнитная волна взаимодействует с зарядами в атомах, составляющих частицу, и таким образом вызывает образование колеблющегося диполя в частице. Рассеяние света означает испускание света во всех направлениях от колеблющегося диполя. При квазиупругом рассеянии света изменения частоты между рассеянным и падающим светом малы, и свет, рассеянный колеблющимся диполем, имеет спектр, который расширяется вокруг частоты падающего света.

Интенсивность рассеянного света зависит от присущих частице физических свойств, таких как размер и молекулярная масса. Интенсивность рассеянного света не является постоянной величиной; она колеблется во времени из-за случайного движения частиц, которые подвергаются броуновскому движению, что означает непрерывное и спонтанное случайное движение частиц в среде, возникающее в результате столкновений между частицами и молекулами среды. Флуктуации интенсивности рассеянного света с течением времени позволяют рассчитать коэффициент диффузии с помощью анализа автокорреляционной функции. Для количественной оценки скорости броуновского движения коэффициент трансляционной диффузии моделируется уравнением Стокса-Эйнштейна. Обратите внимание, что в данном случае коэффициент диффузии обозначается словом 'трансляционный', что указывает на то, что учитывается только трансляционное, но не вращательное движение частицы. Коэффициент трансляционной диффузии имеет единицу площади в единицу времени, где площадь введена для того, чтобы избежать условной смены знака при движении частицы от начала координат. Затем, используя уравнение Стокса-Эйнштейна, по коэффициенту диффузии можно рассчитать распределение частиц по размерам. Этот метод называется динамическим рассеянием света, сокращенно DLS.

Уравнение Стокса-Эйнштейна выражается следующим образом:

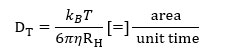
Уравнение 1: Уравнение Стокса-Эйнштейна

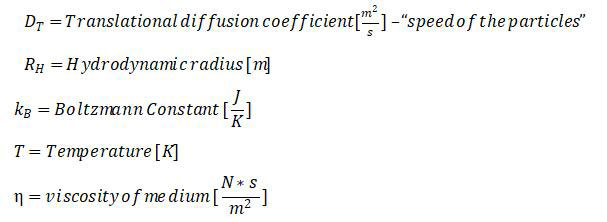
Гидродинамический радиус - это эффективный радиус частицы, которая имеет такую же диффузию, как и идеально сферическая частица этого радиуса. Например, как показано на рисунке 1, истинный радиус частицы - это расстояние между ее центром и внешней окружностью, а гидродинамический радиус включает в себя длину присоединенных сегментов, поскольку они диффундируют как единое целое. Гидродинамический радиус обратно пропорционален коэффициенту трансляционной диффузии.

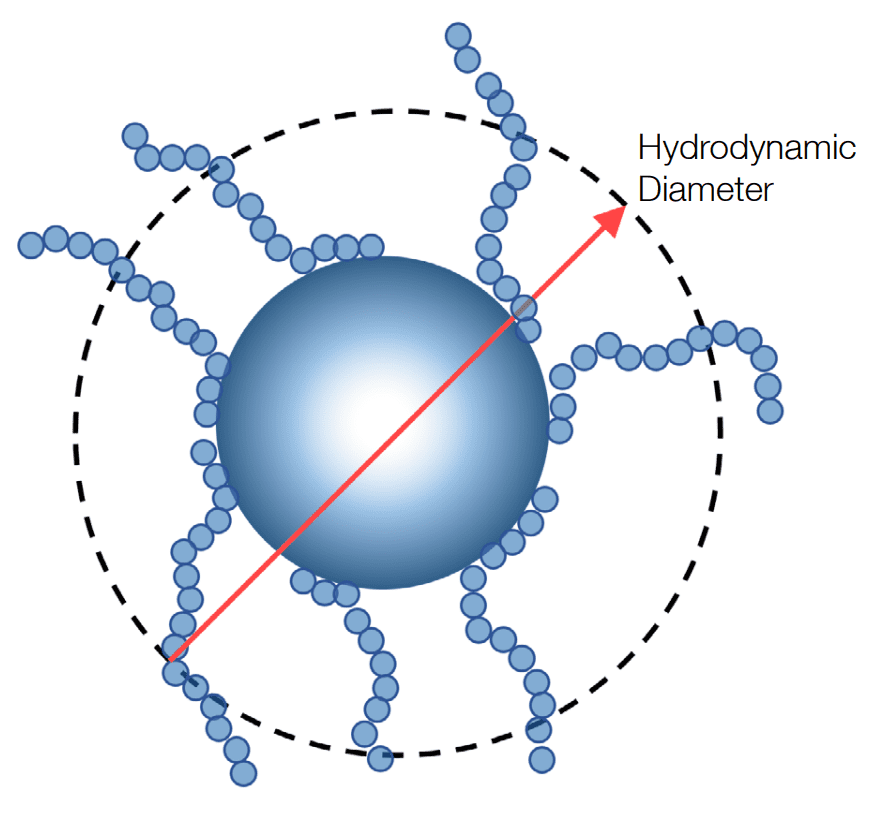
Рисунок 1: Иллюстрация гидродинамического радиуса.

Оптическая настройка

Вся установка прибора DLS показана на рисунке 2.

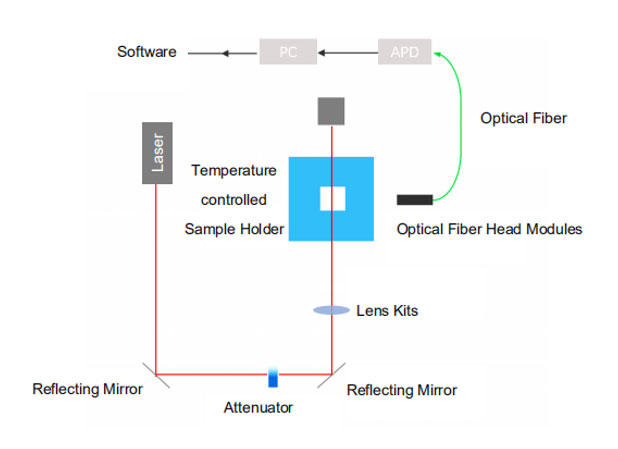
Рисунок 2. Оптическая установка для динамического рассеяния света BeNano 90, Bettersize Instruments.

 
• Лазер
  Большинство лазерных устройств в приборах ДЛС - это газовые и твердотельные лазеры. Типичным примером газового лазера в DLS-установке является гелий-неоновый лазер, излучающий лазер с длиной волны 632,8 нм. Твердотельный лазер относится к лазерным устройствам, в которых в качестве среды усиления выступает твердое тело. В твердотельном лазере в среду усиления добавляют небольшое количество твердых примесей, называемых 'легирующими', чтобы изменить ее оптические свойства. Эти легирующие примеси часто представляют собой редкоземельные минералы, такие как неодим, хром и иттербий. Наиболее часто используемый твердотельный лазер - это легированный неодимом иттриево-алюминиевый гранат, сокращенно Nd: YAG. Преимущества газового лазера - стабильная длина волны излучения при относительно низкой стоимости. Однако газовый лазер обычно имеет относительно большой объем, что делает его очень громоздким. С другой стороны, твердотельный лазер имеет меньший размер и вес, что делает его более удобным в обращении.
 

 
• Детектор
  После того как лазерный луч попадает на ячейку с образцом, свет рассеивается частицами, и этот рассеянный свет колеблется из-за броуновского движения. Высокочувствительный детектор улавливает эти сигналы флуктуации рассеянного света даже при низкой интенсивности и преобразует их в электрические сигналы для дальнейшего анализа в корреляторе. Обычно в оптических установках DLS используются такие детекторы, как фотоэлектронный умножитель и лавинный фотодиод. По данным Лоуренса В.Г. и др., ПМТ и APD имеют схожие характеристики соотношения шума и сигнала на большинстве уровней сигнала, в то время как APD превосходит ПМТ в красной и ближней инфракрасной областях спектра. APD также имеет более высокую абсолютную квантовую эффективность, чем PMT. По этим причинам в последнее время APD все чаще используется в устройствах DLS.
 

 
• Коррелятор
  После оптической настройки завершается процесс рассеивания и сбора интенсивности света. Сигналы, обнаруженные детекторами, затем анализируются в корреляторе для расчета распределения гидродинамического радиуса.
  Мы можем умножить интенсивность рассеяния, собранную детектором, на саму себя после того, как она будет смещена на некоторый произвольный интервал tau (τ) во времени. Этот τ может быть любым - от нескольких наносекунд до микросекунд, но реальное значение временного интервала не влияет на результат теста.
  После применения математического алгоритма можно получить автокорреляционную функцию G1(q, τ). G1(q, τ) одноэкспоненциально убывает от 1 до 0, причем 0 означает полное отсутствие корреляции между сигналами в моменты времени t и t плюс τ, а 1 - идеальную корреляцию. Наконец, имея всю известную информацию о корреляционной функции, можно вычислить гидродинамический радиус с помощью уравнения Стокса-Эйнштейна.
 

Монодисперсный и полидисперсный

Монодисперсные частицы одинаковы по размеру, форме и массе, что приводит к появлению одного узкого пика на кривой распределения частиц по размерам. С другой стороны, полидисперсные частицы не являются однородными по этим параметрам. Важно понимать полидисперсность образцов, поскольку алгоритмы расчета распределения гидродинамического радиуса в корреляторе отличаются в зависимости от того, являются ли образцы монодисперсными или полидисперсными.

Для решения автокорреляционной функции полидисперсных образцов используются два основных математических алгоритма. Первый и наиболее распространенный - метод кумулянтов, который предполагает решение разложения Тейлора автокорреляционной функции. Однако метод кумулянтов применим только для образцов с малым размером полидисперсности. Валидация расчета может быть выполнена путем вычисления и проверки индекса полидисперсности, или PDI, а анализ кумулянтов применим только в том случае, если значение PDI относительно невелико. Алгоритм CONTIN может напрямую вычислить распределение гидродинамического радиуса для образцов, которые широко рассеяны. Это относительно сложный математический метод, включающий регуляризацию.

Интерпретация данных

Интерпретация результатов может помочь нам оценить качество гранулометрического анализа, а также получить информацию о распределении частиц по размерам.
Прежде чем приступать к анализу размера частиц, следует проверить качество корреляционной функции, поскольку оно напрямую связано с точностью результатов анализа размера частиц. Общая форма корреляционной функции может свидетельствовать о ее качестве. Как показано на рисунке 6, если корреляционная кривая представляет собой гладкую кривую, экспоненциально убывающую от 1 до 0, без присутствия шума, это говорит о том, что корреляция была проведена хорошо и можно переходить к анализу распределения частиц по размерам.

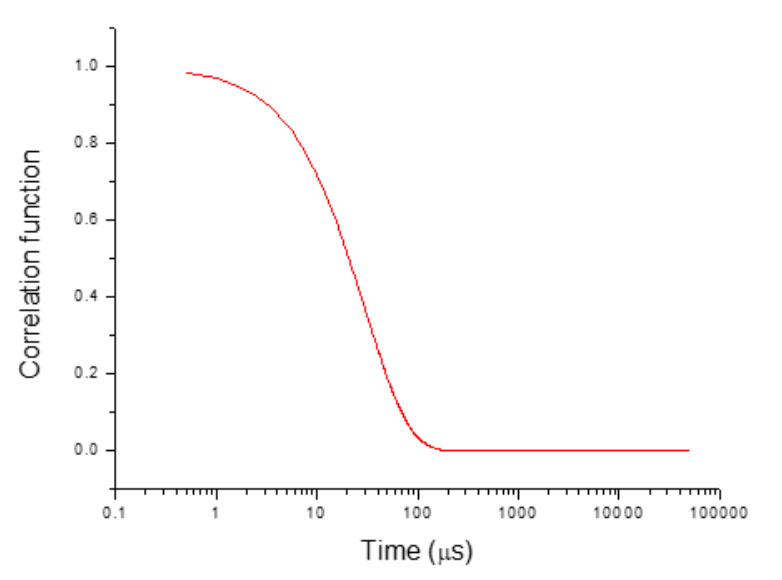
Рисунок 6: Пример хорошей кривой корреляционной функции.

Однако если кривая остается в целом гладкой с некоторым уровнем шума, как показано на рисунке 7, это может быть связано с наличием примесей в образцах, которые влияют на воспроизводимость результатов. В этом случае оператор может снова отфильтровать раствор образца с помощью шприца с соответствующим размером пор, чтобы удалить примеси, такие как крупные частицы пыли в растворе.

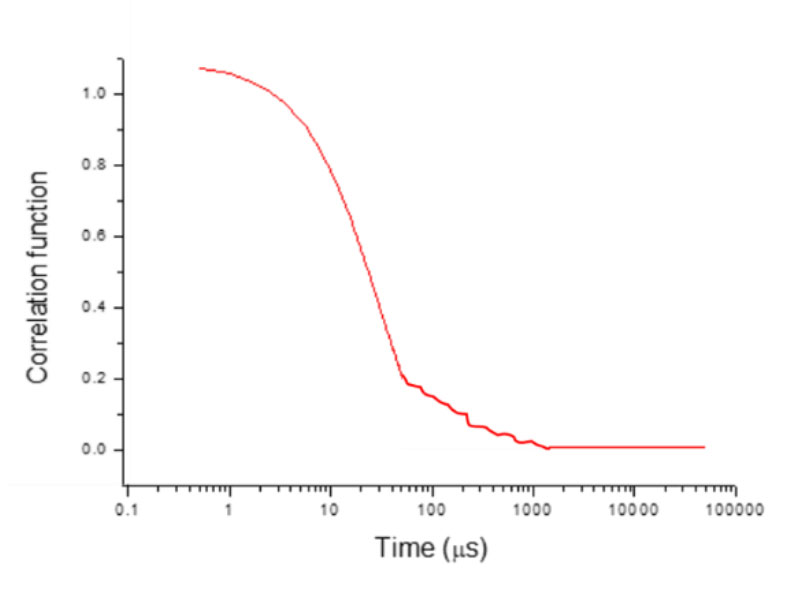
Рисунок 7: Пример кривой корреляционной функции с шумом.

При недостаточном рассеянии в тесте кривая корреляционной функции будет выглядеть как кривая на рисунке 8.

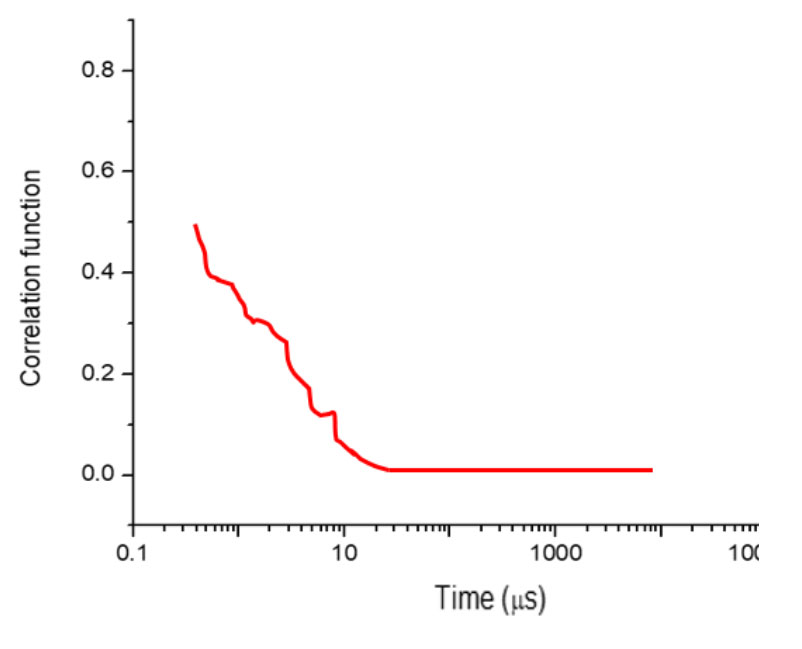
Рисунок 8: Пример плохой кривой корреляционной функции.

В этом случае максимальное значение функции намного меньше 1, и она не демонстрирует экспоненциального распада. Оператор может увеличить концентрацию образца или количество подпрогонов, чтобы увеличить количество рассеивания.

DLS выдает результаты в z-среднем размере частиц, который представляет собой взвешенный по интенсивности рассеяния размер. Это происходит из-за того, что при вычислении интеграла корреляционной функции методом кумулянтов и CONTIN получается средний коэффициент трансляционной диффузии, что приводит к среднему гидродинамическому радиусу из уравнения Стокса-Эйнштейна. Достоверность z-среднего размера частиц следует проверять с помощью индекса полидисперсности или PDI. Как показано в таблице, пример отчета о результатах определения размера частиц с помощью DLS включает в себя z-средний размер частиц с неопределенностью и значение PDI, соответствующее этому z-avg размеру частиц.

Если значение PDI велико, что указывает на возможную полидисперсность образца, то z-средний размер частиц не является полностью репрезентативным описанием данного образца.

Согласно ISO 22412:2017 'Анализ размера частиц при динамическом рассеянии света', результаты определения размера частиц должны быть представлены вместе с их неопределенностью и повторяемостью. Неопределенность измерений выражается стандартным отклонением, а повторяемость - относительным стандартным отклонением, которое описывает, насколько близки друг к другу результаты, полученные в ходе нескольких измерений в каждом цикле испытаний. Согласно ISO 22412:2017, монодисперсные материалы с диаметром от 50 до 200 нм должны иметь размер частиц z-avg с повторяемостью менее 2%.

Ссылка

Чу, Б. Лазерное рассеяние света: Basic Principles and Practice, 2nd ed.; Academic Press: Boston, 1991.

Dian, L.; Yu, E.; Chen, X.; Wen, X.; Zhang, Z.; Qin, L.; Wang, Q.; Li, G.; Wu, C. Enhancing Oral Bioavailability of Quercetin Using Novel Soluplus Polymeric Micelles. Nanoscale Res Lett 2014, 9 (1), 684. https://doi.org/10.1186/1556-276X-9-684.

Dhont, J. K. G. An Introduction to Dynamics of Colloids; Studies in interface science; Elsevier: Amsterdam, Netherlands ; New York, 1996.

Falke, S.; Betzel, C. Динамическое рассеяние света (DLS): Принципы, перспективы, применение к биологическим образцам. In Radiation in Bioanalysis; Pereira, A. S., Tavares, P., Limão-Vieira, P., Eds.; Bioanalysis; Springer International Publishing: Cham, 2019; Vol. 8, pp 173-193. https://doi.org/10.1007/978-3-030-28247-9_6.

ISO 22412:2017. Анализ размера частиц - динамическое рассеяние света (DLS). Международная организация по стандартизации.

Лоуренс, В. Г., Варади, Г., Энтин, Г., Поднесински, Е., и Уоллес, П. К. (2008). Сравнение детекторов на лавинном фотодиоде и фотоэлектронном умножителе для проточной цитометрии. Изображение, манипулирование и анализ биомолекул, клеток и тканей VI. doi:10.1117/12.758958

Рассеяние света от растворов полимеров и дисперсий наночастиц; Springer Laboratory; Springer Berlin Heidelberg: Berlin, Heidelberg, 2007. https://doi.org/10.1007/978-3-540-71951-9.

Nanoscale Informal Science Education Network, NISE Network, Scientific Image - Gold Nanoparticles. Получено с сайта https://www.nisenet.org/catalog/scientific-image-gold-nanoparticles.

Nanoparticles Series, Silicon Nanoparticles Product Details, ACS Materials. Получено с сайта: https://www.acsmaterial.com/silicon-nanoparticles.html.

Оптические датчики, фотоэлектронные умножители, Newport Corporation. Получено с: https://www.newport.com/f/photomultiplier-tubes?q=PMT

Оптоэлектронные компоненты, Лавинные фотодиоды (APD), Warsash Scientific. Получено с сайта: http://www.warsash.com.au/products/optoelectronics/PHOTONIC-DETECTORS.php

Scotti, A.; Liu, W.; Hyatt, J. S.; Herman, E. S.; Choi, H. S.; Kim, J. W.; Lyon, L. A.; Gasser, U.; Fernandez-Nieves, A. The CONTIN Algorithm and Its Application to Determine the Size Distribution of Microgel Suspensions. The Journal of Chemical Physics 2015, 142 (23), 234905. https://doi.org/10.1063/1.4921686.

Технология обнаружения обратного рассеяния

Интеллектуальный поиск оптимальной позиции обнаружения

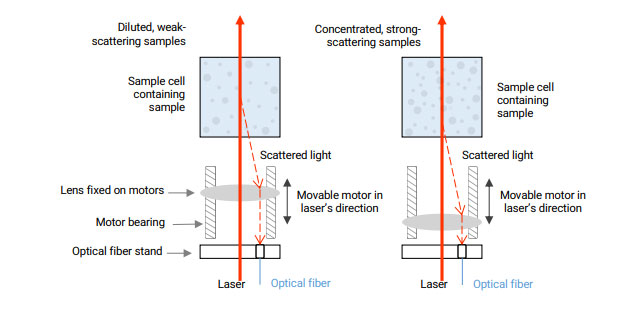
- Точка обнаружения находится в центре ячейки с образцом

Как показано на левом графике, объем обратного рассеяния настолько велик, что детектор получает множество сигналов рассеяния от частиц и, следовательно, повышает чувствительность прибора. Он лучше обнаруживает разбавленные образцы, которые имеют меньший размер и слабый эффект рассеяния. Однако для образцов с очень высокой концентрацией и очень сильным эффектом рассеяния такое обнаружение не подходит. Даже если образец едва обнаружен, результат будет отличаться от истинного значения.

- Точка обнаружения находится на краю ячейки с образцом.

Как показано на правом графике, точка обнаружения фиксируется у стенки ячейки для образцов. Лазерному лучу не нужно проникать в образец, что позволяет эффективно избежать эффекта многократного рассеяния в высококонцентрированных образцах и обеспечить точность и повторяемость результатов определения размера частиц в диапазоне высоких концентраций. Однако из-за оптической конструкции объем рассеивания настолько мал, что ухудшает чувствительность прибора, поэтому при таких условиях прибор не подходит для измерения малых частиц, слабо рассеивающих образцов или очень разбавленных образцов.

Решение: Интеллектуальный поиск оптимальной позиции обнаружения

Перемещая объектив, можно установить точку обнаружения в любом положении от центра до края ячейки с образцом. Это позволяет максимально учесть возможность обнаружения образцов различных типов и концентраций. На практике оптимальная позиция обнаружения и интенсивность лазерного излучения определяются интеллектуально для каждого конкретного образца в соответствии с его концентрацией, размером и способностью к рассеянию, чтобы достичь максимальной точности измерений.