Diffusion dynamique de la lumière

Introduction

La diffusion dynamique de la lumière (DLS), également connue sous le nom de spectroscopie de corrélation de photons (PCS), est une méthode de caractérisation couramment utilisée pour les nanoparticules. L'analyseur de taille de particules DLS présente les avantages de la précision, de la rapidité et d'une bonne répétabilité pour la mesure des nanoparticules, des émulsions ou des suspensions. Le BeNano 180 Zeta Pro est basé sur la diffusion dynamique de la lumière. Il peut mesurer des nanomatériaux jusqu'à 0,3 nanomètre, ce qui est un outil essentiel pour mesurer la distribution de la taille des nanoparticules afin de comprendre et d'étudier les matériaux nanopoudrés.

Contexte théorique

Qu'est-ce que la diffusion de la lumière ? Lorsqu'une source de lumière monochromatique et cohérente irradie la particule, l'onde électromagnétique interagit avec les charges des atomes qui composent la particule et induit ainsi la formation d'un dipôle oscillant dans la particule. La diffusion de la lumière fait référence à l'émission de lumière dans toutes les directions à partir d'un dipôle oscillant. Lors de la diffusion quasi-élastique de la lumière, les changements de fréquence entre la lumière diffusée et la lumière incidente sont faibles, et la lumière diffusée par le dipôle oscillant a un spectre qui s'élargit autour de la fréquence de la lumière incidente.

L'intensité de la lumière diffusée dépend des propriétés physiques intrinsèques de la particule, telles que la taille et le poids moléculaire. L'intensité de la lumière diffusée n'est pas une valeur constante ; elle fluctue dans le temps en raison de la marche aléatoire des particules qui subissent le mouvement brownien, c'est-à-dire la marche aléatoire continue et spontanée des particules lorsqu'elles sont placées dans le milieu, résultant des collisions entre les particules et les molécules du milieu. Les fluctuations de l'intensité de la lumière diffusée en fonction du temps nous permettent de calculer le coefficient de diffusion par l'analyse de la fonction d'autocorrélation. Pour quantifier la vitesse du mouvement brownien, le coefficient de diffusion translationnelle est modélisé par l'équation de Stokes-Einstein. Notez que le coefficient de diffusion est spécifié par le mot 'translationnel', ce qui indique que seul le mouvement de translation, et non de rotation, de la particule est pris en compte. Le coefficient de diffusion translationnelle a l'unité de surface par unité de temps, la surface étant introduite pour éviter la convention de changement de signe lorsque la particule s'éloigne de son origine. En utilisant l'équation de Stokes-Einstein, la distribution de la taille des particules peut être calculée à partir du coefficient de diffusion. Cette technique est appelée diffusion dynamique de la lumière, abrégée en DLS.

L'équation de Stokes-Einstein s'exprime comme suit :

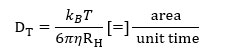
Équation 1 : Équation de Stokes-Einstein

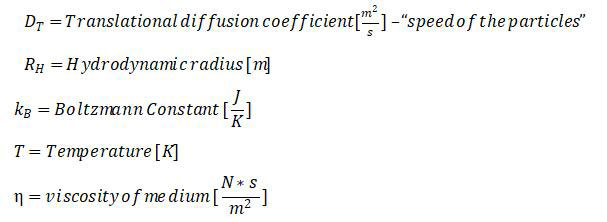
Le rayon hydrodynamique désigne le rayon effectif d'une particule dont la diffusion est identique à celle d'une particule parfaitement sphérique de ce rayon. Par exemple, comme le montre la figure 1, le rayon réel de la particule correspond à la distance entre son centre et sa circonférence extérieure, tandis que le rayon hydrodynamique inclut la longueur des segments attachés puisqu'ils diffusent comme un tout. Le rayon hydrodynamique est inversement proportionnel au coefficient de diffusion translationnelle.

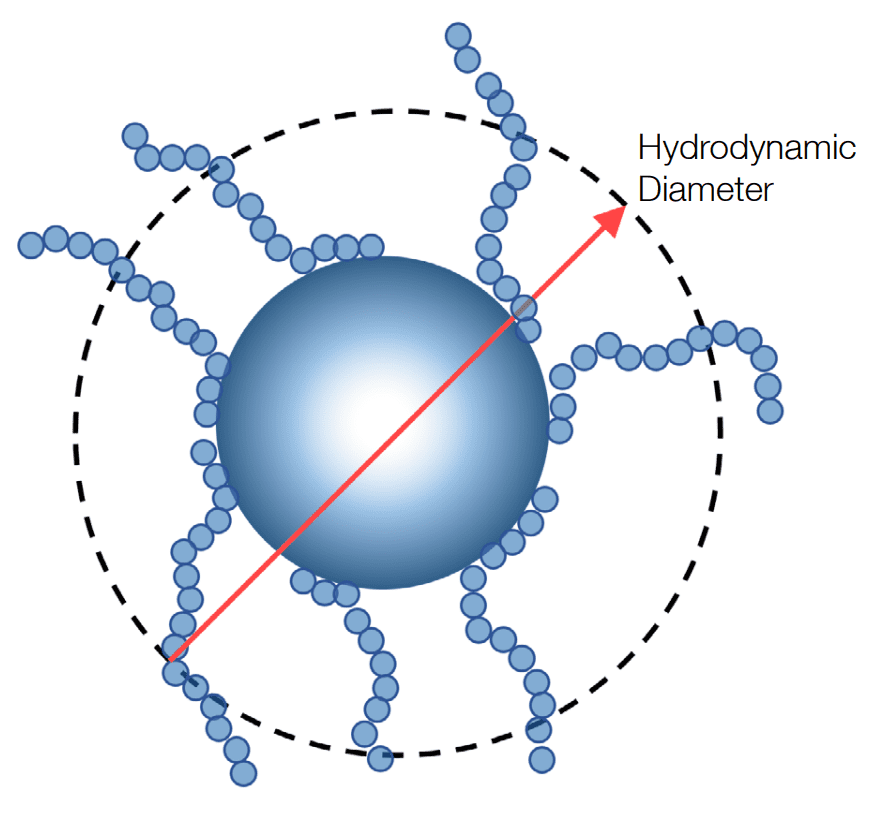
Figure 1 : Illustration du rayon hydrodynamique.

Configuration optique

L'ensemble de la configuration de l'instrument de diffusion dynamique de la lumière est illustré à la figure 2.

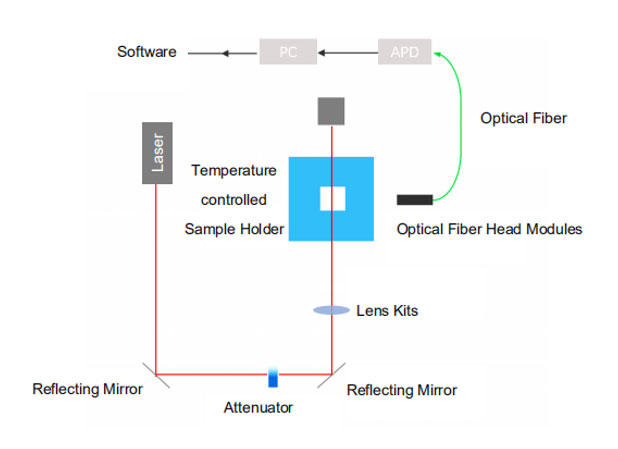
Figure 2 : Installation optique de diffusion dynamique de la lumière du BeNano 90, Bettersize Instruments.

 
• Laser
  La majorité des dispositifs laser dans les instruments DLS sont des lasers à gaz et des lasers à l'état solide. Un exemple typique de laser à gaz dans une installation DLS est le laser hélium-néon qui émet un laser d'une longueur d'onde de 632,8 nm. Un laser à solide se réfère à un dispositif laser dans lequel un solide agit en tant que milieu de gain. Dans un laser à l'état solide, de petites quantités d'impuretés solides appelées 'dopants' sont ajoutées au milieu de gain pour modifier ses propriétés optiques. Ces dopants sont souvent des minéraux de terres rares tels que le néodyme, le chrome et l'ytterbium. Le laser à l'état solide le plus couramment utilisé est le grenat d'aluminium et d'yttrium dopé au néodyme, abrégé en Nd : YAG. Le laser à gaz présente l'avantage d'émettre une longueur d'onde stable à un coût relativement faible. Cependant, un laser à gaz a généralement un volume relativement important qui le rend très encombrant. En revanche, un laser à semi-conducteurs est plus petit et moins lourd, ce qui le rend plus facile à manipuler.
 

 
• Détecteur
  Après l'irradiation du faisceau laser sur la cellule d'échantillonnage, la lumière est diffusée par la particule, et cette lumière diffusée fluctue en raison du mouvement brownien. Un détecteur très sensible capte ces signaux de fluctuations de la lumière diffusée, même à des niveaux de faible intensité, et les convertit en signaux électriques pour une analyse plus poussée dans le corrélateur. Les détecteurs couramment utilisés dans une installation optique de DLS comprennent le tube photomultiplicateur et la photodiode à avalanche. Selon Lawrence W.G. et al, le PMT et l'APD ont un rapport bruit/signal similaire pour la plupart des niveaux de signal, tandis que l'APD l'emporte sur le PMT dans les régions spectrales du rouge et du proche infrarouge. L'APD a également une efficacité quantique absolue supérieure à celle de la PMT. Pour ces raisons, l'APD est de plus en plus utilisé dans les dispositifs DLS.
 

 
• Corrélateur
  Après l'installation optique, le processus de diffusion et de collecte de l'intensité lumineuse est terminé. Les signaux détectés par les détecteurs sont ensuite analysés dans le corrélateur afin de calculer la distribution du rayon hydrodynamique.
  Nous pouvons multiplier l'intensité de diffusion recueillie par le détecteur par elle-même après qu'elle a été décalée d'un intervalle arbitraire tau (τ) dans le temps. Ce τ peut être compris entre quelques nanosecondes et quelques microsecondes, mais la valeur réelle de l'intervalle de temps n'affecte pas le résultat du test.
  L'application de l'algorithme mathématique permet d'obtenir la fonction d'autocorrélation G1(q, τ). G1(q, τ) décroît de manière exponentielle de 1 à 0, 0 signifiant qu'il n'y a aucune corrélation entre les signaux à l'instant t et à l'instant t plus τ, et 1 signifiant une corrélation parfaite. Enfin, avec toutes les informations connues sur la fonction de corrélation, le rayon hydrodynamique peut être calculé à l'aide de l'équation de Stokes-Einstein.
 

Monodisperses et polydisperses

Les particules monodisperses sont toutes identiques en termes de taille, de forme et de masse, ce qui se traduit par un pic étroit dans la courbe de distribution de la taille des particules. En revanche, les particules polydisperses ne sont pas uniformes en ce qui concerne ces paramètres. Il est important de connaître la polydispersité des échantillons car les algorithmes de calcul de la distribution du rayon hydrodynamique dans le corrélateur sont différents selon que les échantillons sont monodisperses ou polydisperses.

Deux algorithmes mathématiques principaux sont utilisés pour résoudre la fonction d'autocorrélation des échantillons polydispersés. Le premier et le plus courant est la méthode des Cumulants, qui consiste à résoudre l'expansion de Taylor de la fonction d'autocorrélation. Toutefois, la méthode Cumulants n'est valable que pour les échantillons dont la polydispersité est faible. La validation du calcul peut être effectuée en calculant et en vérifiant l'indice de polydispersité, ou IPD, et l'analyse Cumulants n'est valable que si la valeur de l'IPD est relativement faible. L'algorithme CONTIN peut calculer directement la distribution du rayon hydrodynamique pour les échantillons largement dispersés. Il s'agit d'une méthode mathématique relativement complexe qui implique une régularisation.

Interprétation des données

L'interprétation des résultats peut nous aider à évaluer la qualité de l'analyse granulométrique et à obtenir des informations sur la distribution granulométrique.
La qualité de la fonction de corrélation doit être vérifiée avant de procéder à l'analyse granulométrique, car elle est directement liée à la précision du résultat. La forme générale de la fonction de corrélation peut indiquer sa qualité. Comme le montre la figure 6, si la courbe de corrélation est une courbe lisse décroissant exponentiellement de 1 à 0 sans présence de bruit, cela suggère que la corrélation a été bien réalisée et qu'il est bon de procéder à l'analyse de la distribution de la taille des particules.

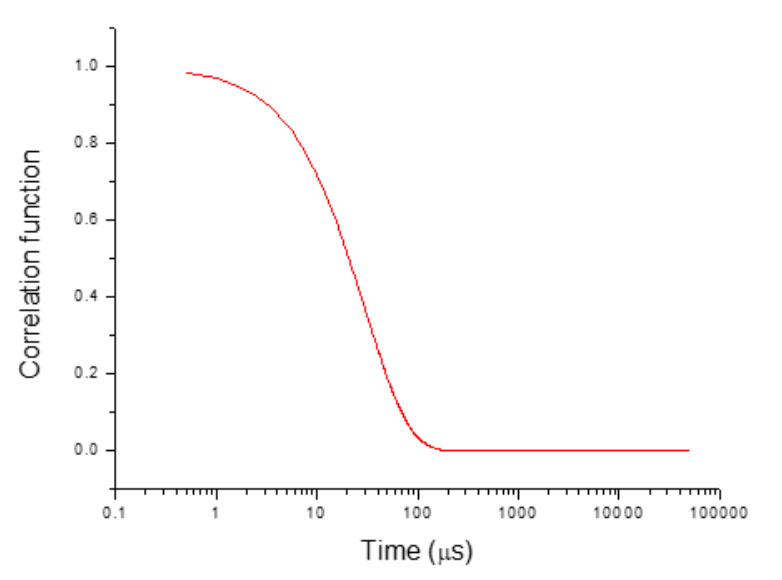
Figure 6 : Exemple d'une bonne courbe de fonction de corrélation.

Toutefois, si la courbe reste globalement lisse avec un certain niveau de bruit, comme le montre la figure 7, cela peut être dû à la présence d'impuretés dans les échantillons qui affectent la répétabilité des résultats. Dans ce cas, l'opérateur peut filtrer à nouveau la solution de l'échantillon avec la seringue de taille de pore appropriée afin d'éliminer les impuretés telles que les grosses particules de poussière présentes dans la solution.

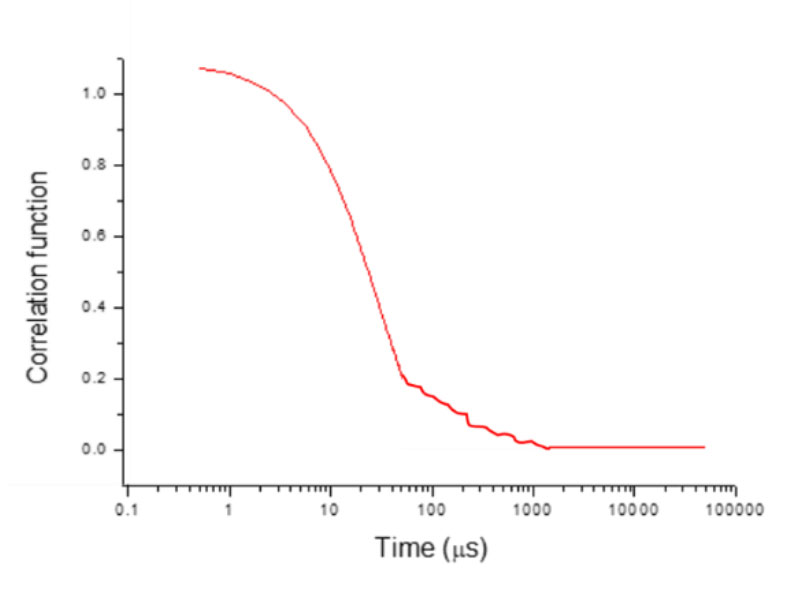
Figure 7 : Exemple d'une courbe de fonction de corrélation avec du bruit.

Lorsque la diffusion est insuffisante dans un test, la courbe de la fonction de corrélation ressemble à la courbe de la figure 8.

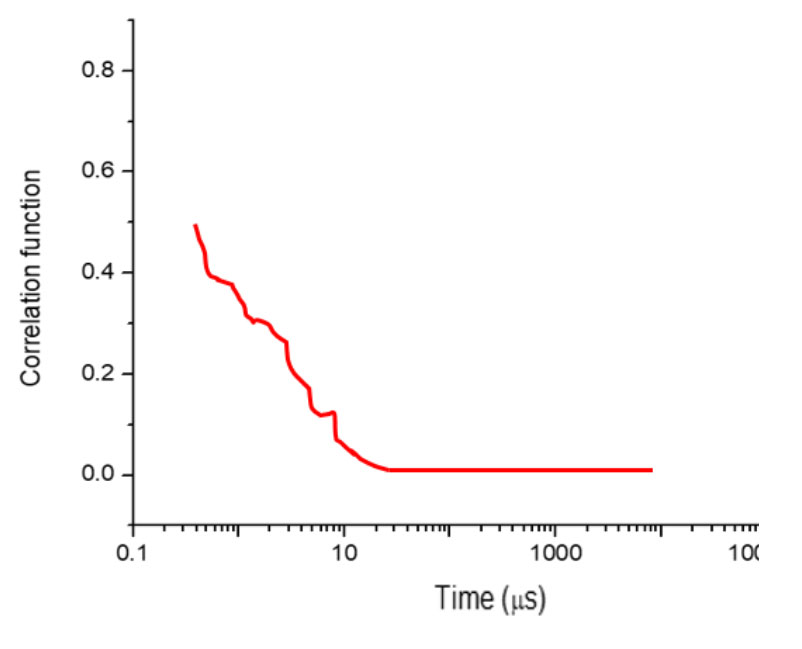
Figure 8 : Exemple d'une courbe de fonction de corrélation médiocre.

Dans ce cas, la valeur maximale de la fonction est bien inférieure à 1 et ne présente pas de comportement de décroissance exponentielle. L'opérateur pourrait augmenter la concentration de l'échantillon ou le nombre de sous-cycles afin d'accroître la diffusion.

La DLS rapporte les résultats en taille moyenne des particules, qui est une taille pondérée par l'intensité de la diffusion. Elle provient du fait que lors du calcul de l'intégrale de la fonction de corrélation à l'aide de la méthode Cumulants et CONTIN, un coefficient moyen de diffusion translationnelle est obtenu, ce qui donne le rayon hydrodynamique moyen de l'équation de Stokes-Einstein. La validité de la taille moyenne des particules en z doit être vérifiée à l'aide de l'indice de polydispersité ou PDI. Comme le montre le tableau, un exemple de rapport de résultats sur la taille des particules provenant de la DLS comprend la taille moyenne z des particules avec l'incertitude et la valeur de l'IPD correspondant à cette taille moyenne z des particules.

Si la valeur de l'IPD est élevée, ce qui indique que les échantillons sont peut-être polydispersés, la taille moyenne des particules n'est pas une description entièrement représentative de l'échantillon donné.

Selon la norme ISO 22412:2017 Analyse granulométrique par diffusion dynamique de la lumière, les résultats relatifs à la taille des particules doivent être rapportés avec leurs incertitudes et leur répétabilité. L'incertitude de mesure est exprimée par l'écart-type, tandis que la répétabilité est l'écart-type relatif qui décrit à quel point les résultats obtenus à partir de mesures multiples sont proches les uns des autres au cours de chaque série d'essais. Conformément à la norme ISO 22412:2017, les matériaux monodispersés dont le diamètre est compris entre 50 et 200 nm doivent avoir une taille de particule z-avg avec une répétabilité inférieure à 2 %.

Référence

Chu, B. Laser Light Scattering : Basic Principles and Practice, 2e édition ; Academic Press : Boston, 1991.

Dian, L. ; Yu, E. ; Chen, X. ; Wen, X. ; Zhang, Z. ; Qin, L. ; Wang, Q. ; Li, G. ; Wu, C. Enhancing Oral Bioavailability of Quercetin Using Novel Soluplus Polymeric Micelles. Nanoscale Res Lett 2014, 9 (1), 684. https://doi.org/10.1186/1556-276X-9-684.

Dhont, J. K. G. An Introduction to Dynamics of Colloids ; Studies in interface science ; Elsevier : Amsterdam, Netherlands ; New York, 1996.

Falke, S. ; Betzel, C. Dynamic Light Scattering (DLS) : Principles, Perspectives, Applications to Biological Samples. In Radiation in Bioanalysis ; Pereira, A. S., Tavares, P., Limão-Vieira, P., Eds ; Bioanalysis ; Springer International Publishing : Cham, 2019 ; Vol. 8, pp 173-193. https://doi.org/10.1007/978-3-030-28247-9_6.

ISO 22412:2017. Analyse de la taille des particules - Diffusion dynamique de la lumière (DLS). Organisation internationale de normalisation.

Lawrence, W. G., Varadi, G., Entine, G., Podniesinski, E. et Wallace, P. K. (2008). A comparison of avalanche photodiode and photomultiplier tube detectors for flow cytometry. Imaging, Manipulation, and Analysis of Biomolecules, Cells, and Tissues VI. doi:10.1117/12.758958

Light Scattering from Polymer Solutions and Nanoparticle Dispersions ; Springer Laboratory ; Springer Berlin Heidelberg : Berlin, Heidelberg, 2007. https://doi.org/10.1007/978-3-540-71951-9.

Nanoscale Informal Science Education Network, NISE Network, Scientific Image - Gold Nanoparticles. Extrait de https://www.nisenet.org/catalog/scientific-image-gold-nanoparticles.

Nanoparticles Series, Silicon Nanoparticles Product Details, ACS Materials. Extrait de : https://www.acsmaterial.com/silicon-nanoparticles.html

Optical Sensors, Photomultiplier Tube, Newport Corporation. Récupéré de : https://www.newport.com/f/photomultiplier-tubes?q=PMT

Composants optoélectroniques, photodiodes à avalanche (APD), Warsash Scientific. Récupéré de : http://www.warsash.com.au/products/optoelectronics/PHOTONIC-DETECTORS.php

Scotti, A. ; Liu, W. ; Hyatt, J. S. ; Herman, E. S. ; Choi, H. S. ; Kim, J. W. ; Lyon, L. A. ; Gasser, U. ; Fernandez-Nieves, A. The CONTIN Algorithm and Its Application to Determine the Size Distribution of Microgel Suspensions. The Journal of Chemical Physics 2015, 142 (23), 234905. https://doi.org/10.1063/1.4921686.

Technologie de détection par rétrodiffusion

Avec recherche intelligente de la position de détection optimale

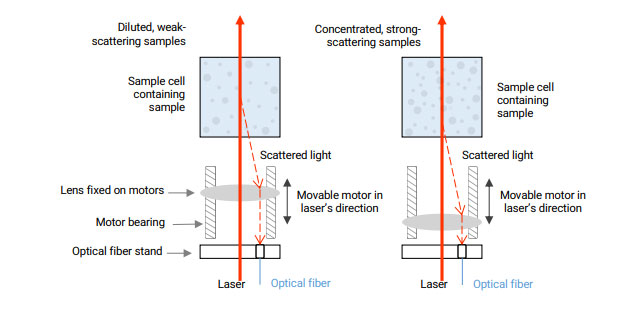
- Le point de détection se trouve au milieu de la cellule d'échantillonnage.

Comme le montre le graphique de gauche, le volume de rétrodiffusion est si important que le détecteur reçoit de nombreux signaux de diffusion des particules, ce qui augmente la sensibilité de l'instrument. La capacité de détection est meilleure pour les échantillons dilués, qui ont des tailles plus petites et des effets de diffusion plus faibles. Cependant, la détection n'est pas viable pour les échantillons ayant des concentrations extrêmement élevées et des effets de diffusion très importants. Même si l'échantillon est à peine détecté, le résultat s'écartera de la valeur réelle.

- Le point de détection se trouve au bord de la cellule d'échantillonnage

Comme le montre le graphique de droite, le point de détection est fixé près de la paroi de la cellule d'échantillonnage. Le faisceau laser n'a pas besoin de pénétrer dans l'échantillon, ce qui permet d'éviter efficacement l'effet de diffusion multiple des échantillons à forte concentration et de garantir la précision et la répétabilité des résultats relatifs à la taille des particules dans la plage de concentration élevée. Toutefois, en raison de sa conception optique, le volume de diffusion est si petit qu'il réduit la sensibilité de l'instrument, qui n'est donc pas en mesure de mesurer les petites particules, les échantillons à faible diffusion ou les échantillons très dilués dans ces conditions.

La solution : Recherche intelligente de la position de détection optimale

En déplaçant la lentille, le point de détection peut être placé à n'importe quel endroit, du centre au bord de la cellule d'échantillonnage. Cela permet de prendre en compte, dans la mesure du possible, la détection de différents types et concentrations d'échantillons. Dans la pratique, la position de détection optimale et l'intensité du laser sont déterminées intelligemment pour chaque échantillon spécifique en fonction de sa concentration, de sa taille et de sa capacité de diffusion afin d'obtenir la plus grande précision de mesure.