Influence de la taille des particules et de la densité réelle des microsphères de verre creuses sur la résistance à la compression
2024-03-15Application Note
Cette note d'application explore la corrélation entre la taille des particules, la densité réelle et la résistance à la compression des microsphères de verre creuses (HGM). En utilisant l'analyseur de taille de particules par diffraction laser Bettersizer 2600 et le pycnomètre à gaz BetterPyc 380, elle confirme que la taille des particules et la densité réelle affectent la résistance à la compression. Les informations fournies par Bettersize contribuent de manière significative au domaine de l'ingénierie des matériaux HGM.
| Produit | Bettersizer 2600Pycnomètre à gaz, BetterPyc 380 |
| Secteur d'activité | Céramique |
| Échantillon | Microsphère creuse en verre |
| Type de mesure | Taille des particules, Distribution des particules, Densité réelle |
| Technologie de mesure | Diffraction laser, méthode de déplacement des gaz |
Aller à une section :
Introduction
Les microsphères creuses de verre (HGM) sont des matériaux sphériques inorganiques non métalliques fabriqués selon des procédés spécifiques, dont le diamètre varie généralement de 10 à 250 µm et l'épaisseur de la paroi de 1 à 2 µm, comme le montre la figure 1. Ces microsphères sont réputées pour leurs propriétés exceptionnelles, telles que la résistance à l'abrasion et à la corrosion, la protection contre les radiations, la faible absorption d'eau et la stabilité chimique. Elles peuvent être largement utilisées comme matériaux composites dans la construction, le caoutchouc, les revêtements, la marine, l'aérospatiale et d'autres domaines. La résistance à la compression des HGM est un paramètre physique crucial qui influence directement leur applicabilité et la qualité des produits finis dans divers domaines.
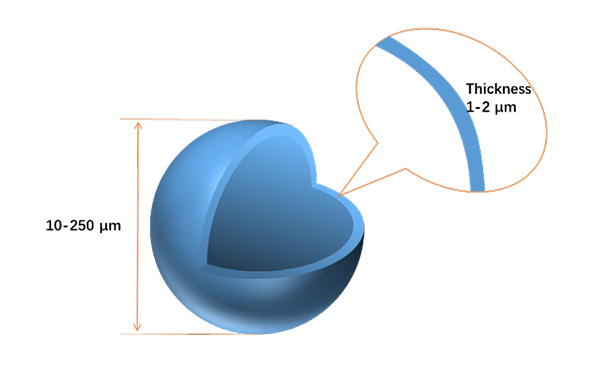
Figure 1. Structure des HGM
Selon la formule théorique de résistance à la rupture d'une microsphère de verre creuse individuelle [1,2] :
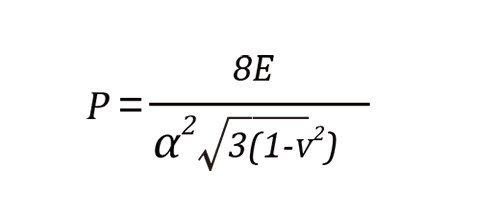
P est la résistance à la compression
α est le facteur de forme (le rapport entre le diamètre D et l'épaisseur de la paroi t)
E est le module d'Young théorique de la microsphère de verre creuse
ν est le coefficient de Poisson des matériaux de la paroi
La résistance à la compression des HGM est liée au diamètre D et à l'épaisseur de la paroi t, car ces facteurs influencent collectivement le facteur de forme. La poudre de HGM étant constituée de nombreuses particules de tailles différentes, l'effet global de la taille et de la distribution des particules doit être pris en compte. La mesure directe de l'épaisseur de la paroi des HGM est une tâche qui prend du temps, mais l'évaluation de son épaisseur par la mesure de la densité réelle sera plus facile à réaliser. La mesure et l'analyse précises de la distribution de la taille des particules et de la densité réelle des poudres de HGM permettent de mieux comprendre leurs performances dans différentes applications, d'optimiser la quantité et les méthodes de remplissage et d'améliorer encore les performances et la stabilité des matériaux composites.
Méthode de mesure
Cette étude a utilisé l'analyseur de taille de particules par diffraction laser Bettersizer 2600 et le pycnomètre à gaz BetterPyc 380 pour étudier la distribution de la taille des particules et la densité réelle de quatre ensembles de formulations identiques de HGM. Les résultats des tests ont été analysés afin d'explorer la relation entre la résistance à la compression, la distribution de la taille des particules et la densité réelle.
Le Bettersizer 2600, basé sur la théorie de Mie (conforme à la norme ISO 13320), permet d'obtenir rapidement des informations sur la taille et la distribution des particules en mesurant l'angle de diffraction et l'intensité des particules par rapport au laser, comme le montre la figure 2. Il offre des vitesses d'essai rapides, les résultats étant disponibles en 1 minute seulement. Avec la méthode humide, l'indice de réfraction des HGM et du milieu solvant (eau distillée) était respectivement de 1,46 et de 1,33.
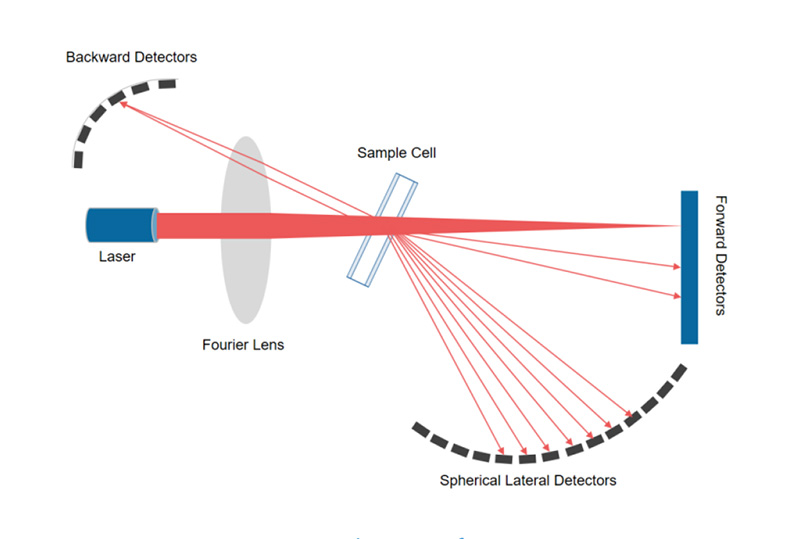
Figure 2. Schéma du système du Bettersizer 2600
Le pycnomètre à gaz BetterPyc 380 est basé sur l'équation de l'état des gaz idéaux et utilise la méthode de déplacement des gaz (conforme à la norme ISO 12154:2014) avec un système de contrôle de la température. Il permet de mesurer le volume des HGM et, par la suite, leur densité réelle. L'hélium est utilisé comme gaz d'analyse dans cette étude, avec des mesures effectuées à des pressions de 19,5 psig et un taux d'équilibre contrôlé de 0,005 psig/min à une température de 20. L'instrument offre des vitesses de test rapides et fonctionne de manière non destructive, ce qui en fait une méthode efficace et fiable pour tester la densité.
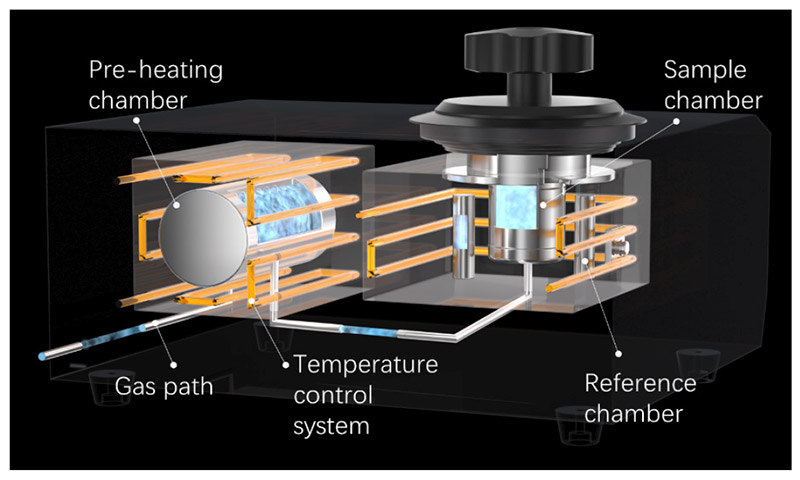
Figure 3. Schéma du système BetterPyc 380
Résultat
Le tableau 1 présente les données relatives à la taille des particules et à la densité réelle de quatre groupes d'échantillons. On observe que les échantillons HGM-1 et HGM-2 ont des tailles de particules et des distributions similaires, avec des densités réelles de 0,6033 g/cm3 et 0,3842 g/cm3 respectivement. Leurs résistances à la compression sont respectivement de 83 MPa et 38 MPa. Selon la formule théorique de résistance à la rupture, lorsque le diamètre reste constant, une densité réelle plus élevée indique une épaisseur de paroi plus importante, ce qui se traduit par un facteur de forme plus faible et, par conséquent, une résistance à la compression plus élevée. Les résultats expérimentaux correspondent bien aux attentes théoriques.
| Échantillon | Distribution de la taille des particules (µm) | Densité réelle (g/cm3 ) | Résistance à la compression (MPa) | ||
| D10 | D50 | D90 | |||
| HGM-1 | 16.62 | 40.57 | 79.76 | 0.6033 | 83 |
| HGM-2 | 16.34 | 40.48 | 79.82 | 0.3842 | 38 |
| HGM-3 | 12.09 | 20.43 | 33.12 | 0.5033 | 110 |
| HGM-4 | 4.51 | 10.11 | 21.06 | 0.7824 | 207 |
Tableau 1. Distribution de la taille des particules, densité réelle et résistance à la compression des échantillons de HGM.
En comparant les échantillons HGM-2, HGM-3 et HGM-4, comme l'illustre la figure 4, il apparaît que lorsque la taille des particules D50 diminue, la densité réelle (indiquée par l'épaisseur de la paroi) augmente progressivement, ce qui signifie que le facteur de forme est plus faible. Ce phénomène explique l'augmentation de la résistance à la compression. Cette observation souligne l'importance de la taille et de la densité des particules dans la détermination des propriétés mécaniques des microsphères de verre creuses.
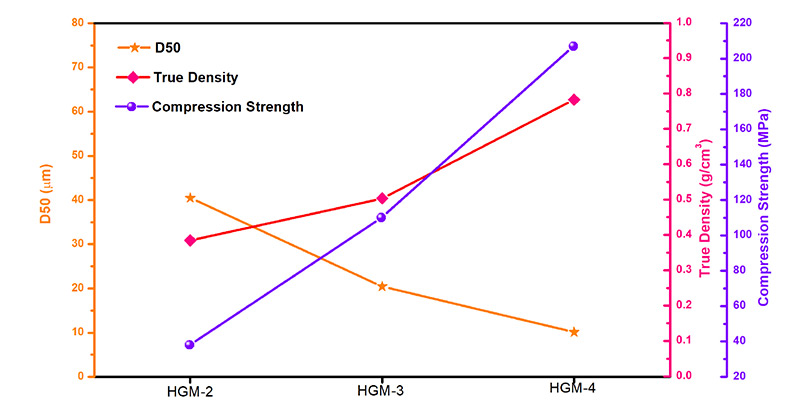
Figure 4. D50, densité réelle et résistance à la compression de HGM-2, HGM-3 et HGM-4
Conclusion
En résumé, pour des HGM ayant la même formulation, le contrôle de différentes gammes de tailles de particules par tamisage permet de produire des échantillons présentant des caractéristiques de résistance variées. Pour répondre à des critères spécifiques de taille de particules, l'optimisation du processus pour améliorer la densité réelle des microsphères de verre creuses est une approche viable, qui peut potentiellement améliorer leur résistance à la compression. L'analyseur granulométrique laser Bettersizer 2600 et le pycnomètre à gaz BetterPyc 380 conçus par Bettersize peuvent fournir des références et un contrôle essentiels pour la conception des matériaux et les applications d'ingénierie.
 Bettersizer 2600 Bettersizer 2600 |  BetterPyc 380 BetterPyc 380 |
Références
[1] P.W. Bratt, J. Cunnion, B.D. Spivack, Advances in Materials Characterization 441 (1983).
[2] S.P. Timoshenko, J.M. Gere, Theory of Elastic Stability, McGraw-Hill, New York, 1961.
À propos des auteurs
 | Perfil Liu Ingénieur d'application principal @ Bettersize Instruments |
 | Yanling Qu Ingénieur d'application @ Bettersize Instruments |
| Vous souhaitez obtenir des matériaux céramiques de haute performance ? |  |
Recommended articles
Rate this article
