Comment déterminer la moyenne, la médiane et le mode ?

La médiane est la valeur centrale d'une liste de valeurs classées de la plus petite à la plus grande.

Le mode est la valeur la plus fréquente dans la liste des valeurs.

La moyenne est calculée en additionnant les valeurs de la liste et en divisant la somme totale des valeurs par le nombre de valeurs de la liste. La formule ci-dessous en est la meilleure description.

La moyenne, notée ¯x , d'un ensemble de n valeurs _x1, _x2, ..._xn, est définie comme la somme des nombres divisée par :

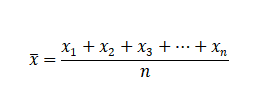
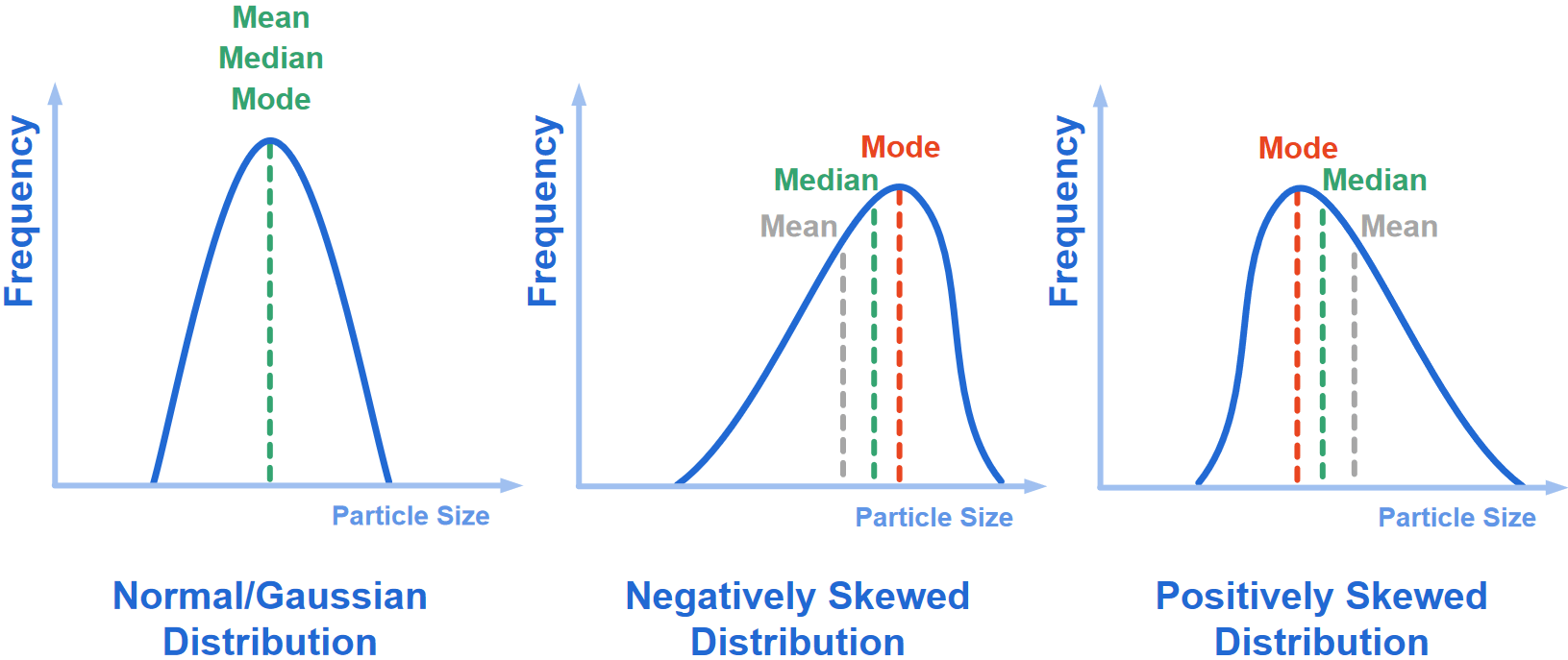
La distribution normale/gaussienne illustrée ci-dessous montre que la moyenne, la médiane et le mode ont tous la même valeur. En outre, une distribution normale/gaussienne comporte des valeurs qui, plus elles sont proches de la moyenne, plus elles sont fréquentes que les valeurs qui en sont éloignées. Ainsi, la valeur moyenne = la valeur médiane = la valeur du mode = la valeur D50 = la valeur de 50 %.

Les valeurs du mode et de la moyenne sont différentes de la médiane pour les distributions asymétriques négatives et positives.

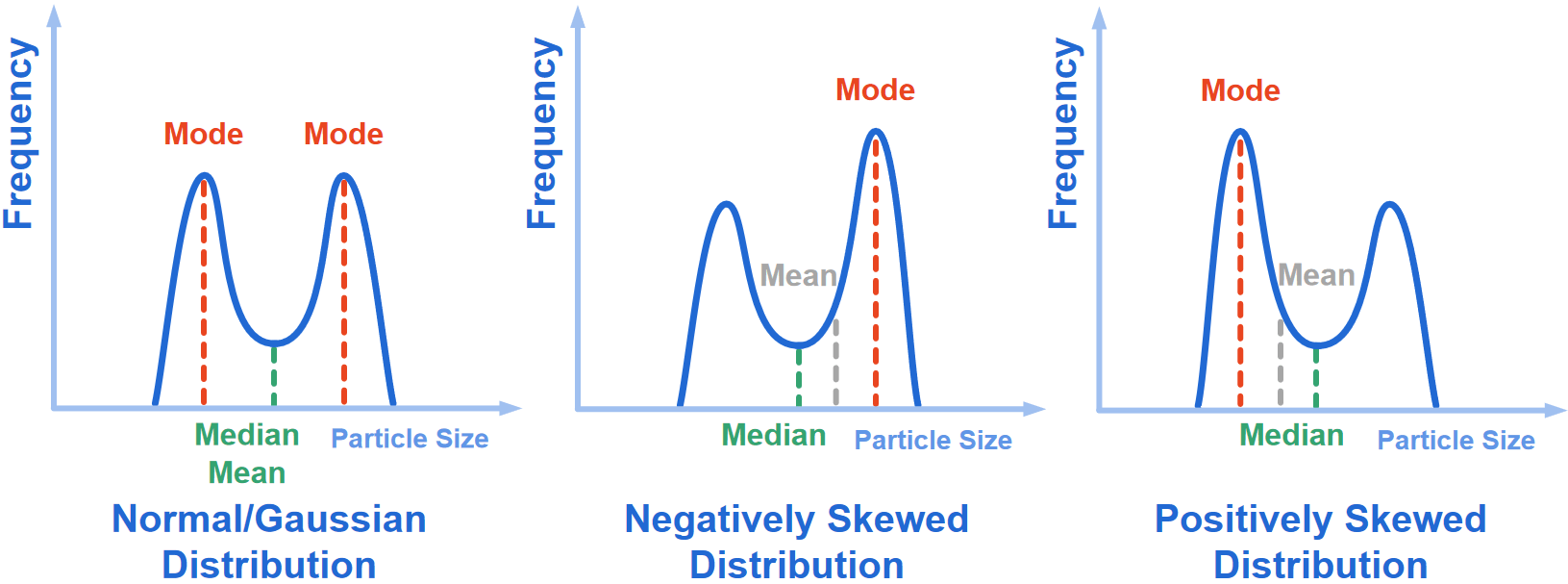
La distribution normale/gaussienne, les distributions négativement et positivement asymétriques pour une distribution bimodale sont illustrées ci-dessous.

Vous avez du mal à comprendre les concepts de l'analyse de particules ? Notre nouveau Guide d'initiation à l'analyse des particules est là pour vous aider à appréhender ces concepts de la manière la plus accessible possible. Téléchargez-le au format PDF pour le lire dans le train, l'avion ou tout autre endroit où il n'y a pas d'Internet..